Chemistry I
Chapter 1R: Review
Units of Measurement
How do you quantify time? Depends on the application.
- 30 s (in the microwave)
- 50 min (of class)
- 10 h (until bedtime)
- 7 d (until next Friday)
- 4 m (until your birthday)
- 3 y (until graduation)
Measurement System
How do you quantify a length?
Imperial System of Measurement
- in (relatively small lengths)
- ft
- yd
- mile (relatively big lengths)
Metric System
- millimeter (relatively small lengths)
- centimeter
- meter
- kilometer (relatively big lengths)
Metric System
Some countries still use the imperial system. Science has adopted the metric system, a system of measurement that uses units with ratios that are multiples of 10.
Source: Wikimedia
SI Base Units
Science uses SI Units (International System of Units) to describe quantities. The base SI units are as follows:
Metric Prefixes
Used to modify a basic unit
| Prefix | Abbeviation | Meaning | Example |
|---|---|---|---|
Tera- |
T |
1012 (trillion) |
1 terameter (Gm) = 1×1012 m |
Giga- |
G |
109 (billion) |
1 gigameter (Gm) = 1×109 m |
Mega- |
M |
106 (million) |
1 megameter (Mm) = 1×106 m |
Kilo- |
k |
103 (thousand) |
1 kilometer (km) = 1×103m |
Deci- |
d |
10–1 (one tenth) |
1 decimeter (dm) = 1×10–1 m |
Centi- |
c |
10–2 (one hundredth) |
1 centimeter (cm) = 1×10–2 m |
Milli- |
m |
10–3 (one thousandth) |
1 millimeter (mm) = 1×10–3 m |
Micro- |
μ |
10–6 (one millionth) |
1 micrometer (μm) = 1×10–6 m |
Nano- |
n |
10–9 (one billionth) |
1 nanometer (nm) = 1×10–9 m |
Pico- |
p |
10–12 (one trillionth) |
1 picometer (pm) = 1×10–12 m |
Femto- |
f |
10–15 |
1 femtometer (fm) = 1×10–16 m |
Example
Which quantity would be most appropriate for describing the distance between Athens, GA and Akron, OH (ca. 665 mi)?
- 1.07×108 cm (107 million cm)
- 1.07×106 m (1.07 million m)
- 1,069 km (1.07 thousand km)
Temperature
Temperature Scales
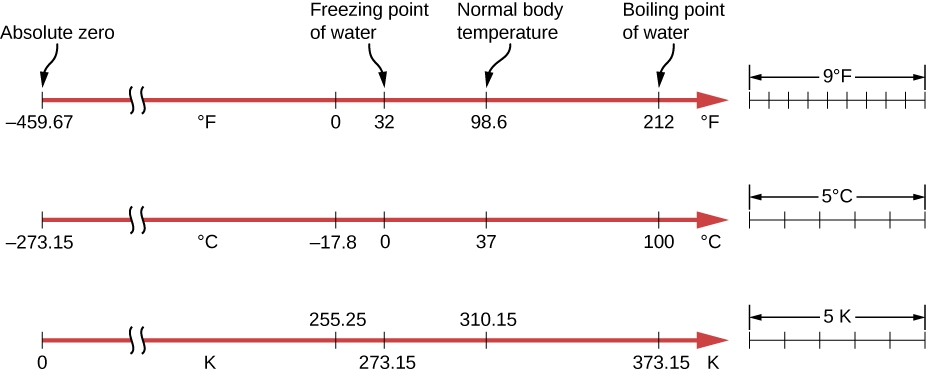
Source: Openstax
Temperature Conversions
°F → °C
\[t/^{\circ}\mathrm{C} = \dfrac{\left ( t/^{\circ}\mathrm{F} - 32 \right )}{1.8}\]
°C → K
\[t/\mathrm{K} = t/^{\circ}\mathrm{C} + 273.15\]
°C → °F
\[t/^{\circ}\mathrm{F} = \left ( t/^{\circ}\mathrm{C} \times 1.8 \right ) + 32\]
K → °C
\[t/^{\circ}\mathrm{C} = t/\mathrm{K} - 273.15\]
Practice – Temperature
What is 93.0 °F in °C and K?
33.9 °C
Practice – Temperature
What is absolute zero (0 K) in °C and °F?
–273.15 °C
Exponents
\[b^n = \underbrace{b \times b \times \cdots \times b}_{n~\mathrm{times}}\]
\[10^1 = 10 \] \[10^2 = 10 \times 10 = 100\] \[10^3 = 10 \times 10 \times 10 = 1000\]
Exponents
\[b^{-n} = \underbrace{\dfrac{1}{b} \times \dfrac{1}{b} \times \cdots \times \dfrac{1}{b}}_{n~\mathrm{times}}\]
\[10^{-1} = \dfrac{1}{10} = 0.1\] \[10^{-2} = \dfrac{1}{10} \times \dfrac{1}{10} = 0.01\]
\[10^{-3} = \dfrac{1}{10} \times \dfrac{1}{10} \times \dfrac{1}{10} = 0.001\]
Scientific Notation
Used for small and big numbers
\[ 1,234 = 1.234\times 10^1 \times 10^1 \times 10^1 = 1.234\times 10^3 \]
\[ 0.01234 = 1.234 \times 10^{-1} \times 10^{-1} = 1.234\times 10^{-2} \]
\[ 0.1234 = \dfrac{1.234}{10^1\times 10^1} = 1.234\times 10^{-2} \]
Practice
Write the following numbers into scientific notation.
\[502\]
\[1,535,234\]
\[0.00008753\]
\[5.02\times 10^2\]
\[1.535234 \times 10^{6}\]
\[8.753\times 10^{-5}\]
Sci. Notation: Add and Subtract
\[3.4\times 10^{4} + 9.7\times 10^{5}\]
Transform each number into the same power of 10.
\[0.34\times 10^{5} + 9.7\times 10^{5}\]
Add or subtract the numbers.
\[10.04\]
Rewrite in scientific notation.
\[10.04 \times 10^{5} = 1.004 \times 10^6\]
Sci. Notation: Multiplying
Powers of 10 get added.
\[200 \times 100 = 20,000 = 2.00\times 10^{4}\]
\[\begin{align*} \left (2.00\times 10^{2} \right) \times \left (1.00 \times 10^{2}\right) &= \\[2ex] \left (2.00\times 1.00 \times 10^{2} \times 10^{2} \right) &= 2.00\times 10^4 \end{align*}\]
Sci. Notation: Dividing
Powers of 10 get subtracted.
\[\begin{align*} \dfrac{200}{100} = 2 &= 2\times 10^{0} \\[4ex] \dfrac{2.00\times 10^{2}}{1.00 \times 10^{2}} &= 2\times 10^0 = 2 \end{align*}\]
Significant Figures (digits)
Not all digits are significant. Here, the graduated cylinder is a “measuring stick” for volume. How accurate are we able to make a reading?
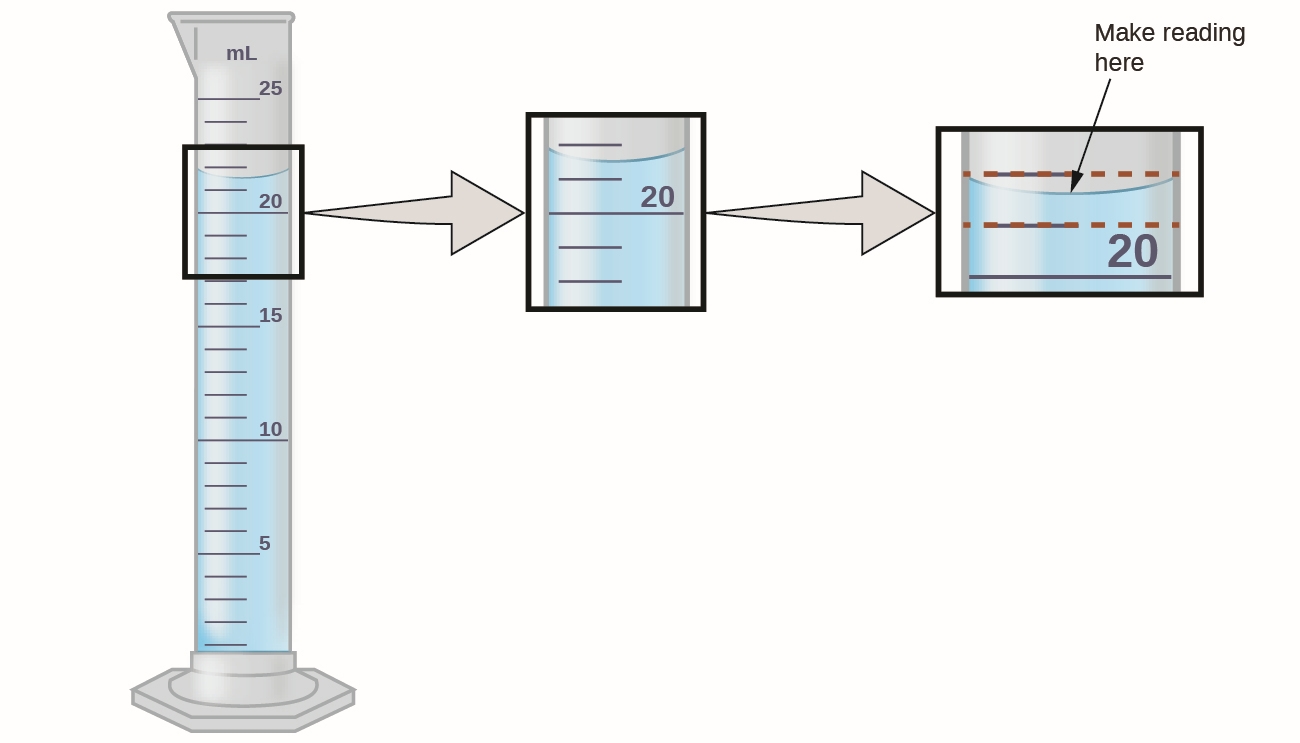
Significant Figures (digits)
We know by inspection that the water is clearly greater than 21 mL but less than 22 mL. We estimate that the water is perhaps 21.6 mL (at the meniscus).

The “2” and the “1” are certain but the 0.6 is uncertain. All certain/exact digits as well as the first uncertain/inexact digit are considered significant. Our measurement has three significant figures.
Source: Openstax
Significant Figures
The numbers you use in this class are treated as exact (infinite sig. figs.) or inexact numbers.
Exact
Obtained through counting
- 3 pennies
- 15 puppies
- 130 students
Inexact
Obtained through measurement
- length
- mass
- volume
- temperature
Unit Conversions
Imperial-to-metric conversions
- Hard – inexact; conversion
- Soft – exact; substitution
See table for some official SI Units and Conversions
For this class, treat all imperial-to-metric conversions as being exact.
See Conversions notes.
Measurements
Precision - indicates how well several measurements agree
Accuracy - the agreement of a measurement with the accepted value
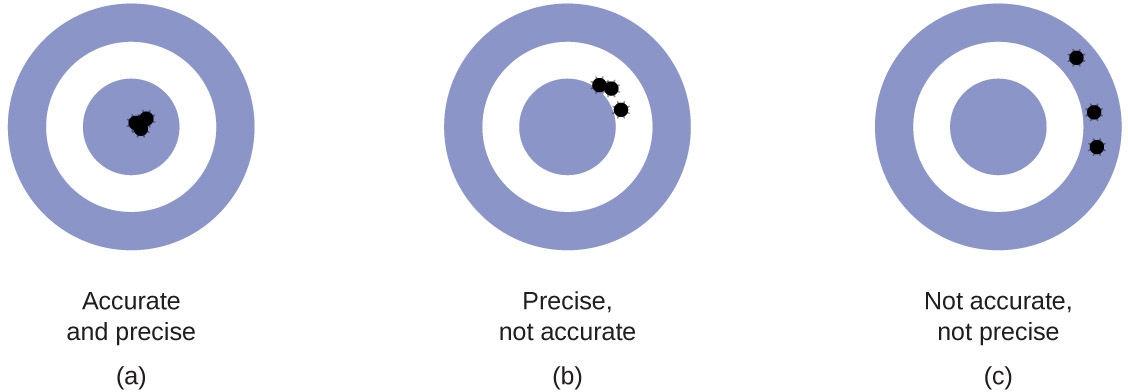
Source: Openstax
Error
Measurements have error.
Experimental Error
“Error in measurement” can be an average value of n measurements.
\[\mathrm{error~in~measurement} = \mathrm{measured~value} - \mathrm{accepted~value}\]
Percent Error
\[ \%~\mathrm{error} = \dfrac{\mathrm{error~in~measurement}}{\mathrm{accepted~value}}\times 100\% \]
Practice
A coin has a diameter of 28.054 mm. Two people make a series of measurements (reported in mm). What is the average diameter and percent error obtained in each case? Which person was more accurate on average?
| Person 1 | Person 2 |
|---|---|
28.246 |
27.9 |
28.244 |
28.0 |
28.246 |
27.8 |
28.248 |
28.1 |
Person 1
Average: 28.246 mm
\[\begin{align*} \mathrm{\%~error} &= \dfrac{28.246~\mathrm{mm} - \mathrm{28.054~\mathrm{mm}}}{28.054~\mathrm{mm}}\\[1.5ex] &~~~~\times 100\% \\[1.5ex] &= 0.684\% \end{align*}\]
Person 2
Average: 27.95 mm
\[\begin{align*} \mathrm{\%~error} &= \dfrac{27.\bar{9}5~\mathrm{mm} - \mathrm{28.054~\mathrm{mm}}}{28.054~\mathrm{mm}}\\[1.5ex] &~~~~\times 100\% \\[1.5ex] &= -0.4\% \end{align*}\]
Press q for answer.
Types of Error
Determinate
identifiable; can be avoided
- using impure reagents
- underwashing glassware
- overwashing precipitates
- careless measuring
Indeterminate
random; arises from uncertainties in measurements
- random fluctuations in measuring devices (e.g. background noise from signals)
Standard Deviation
The std. dev. of a series of measurements is equal to the
- square root of the sum (\(\Sigma\)) of the squares of the deviations (\(\left ( x_i - \bar{x} \right )^2\)) for each measurement (\(x_i\)) from the average (\(\bar{x}\))
- divided by one less than the number, N, of measurements
\[\mathrm{std.~dev.} = \sqrt{\dfrac{\sum{\left(x_i - \bar{x}\right)^2}}{N-1}}\]
